Continuum

All the arguments of Zeno depend on supposing that a continuum has ultimate parts. But a continuum is precisely that, every part of which has parts, in the same sense.

We now come to the difficult question, What is continuity? Kant confounds it with infinite divisibility, saying that the essential character of a continuous series is that between any two members of it a third can always be found. This is an analysis beautifully clear and definite; but, unfortunately, it breaks down under the first test. For according to this, the entire series of rational fractions arranged in the order of their magnitude would be an infinite series, although the rational fractions are numerable, while the points of a line are innumerable. Nay, worse yet, if from that series of fractions any two with all that lie between them be excised, and any number of such finite gaps be made, Kant’s definition is still true of the series, though it has lost all appearance of continuity.

[—]

Kant’s definition expresses one simple property of a continuum; but it allows of gaps in the series. To mend the definition, it is only necessary to notice how these gaps can occur. Let us suppose, then, a linear series of points extending from a point, A, to a point, B, having a gap from B to a third point, C, and thence extending to a final limit, D; and let us suppose this series conforms to Kant’s definition. Then, of the two points, B and C, one or both must be excluded from the series; for otherwise, by the definition, there would be points between them. That is, if the series contains C, though it contains all the points up to B, it cannot contain B. What is required, therefore, is to state in non-metrical terms that if a series of points up to a limit is included in a continuum the limit is included. It may be remarked that this is the property of a continuum to which Aristotle’s attention seems to have been directed when he defines a continuum as something whose parts have a common limit. The property may be exactly stated as follows: If a linear series of points is continuous between two points, A and D, and if an endless series of points be taken, the first of them between A and D and each of the others between the last preceding one and D, then there is a point of the continuous series between all that endless series of points and D, and such that every other point of which this is true lies between this point and D. For example, take any number between 0 and 1, as 0.1; then, any number between 0.1 and 1, as 0.11; then any number between 0.11 and 1, as 0.111; and so on, without end. Then, because the series of real numbers between 0 and 1 is continuous, there must be a least real number, greater than every number of that endless series. This property, which may be called the Aristotelicity of the series, together with Kant’s property, or its Kanticity, completes the definition of a continuous series.

The property of Aristotelicity may be roughly stated thus: a continuum contains the end point belonging to every endless series of points which it contains. An obvious corollary is that every continuum contains its limits. But in using this principle it is necessary to observe that a series may be continuous except in this, that it omits one or both of the limits.

Let us now consider what is meant by saying that a line, for example, is continuous. The multitude of points, or limiting values of approximations upon it, is of course innumerable. But that does not make it continuous. Kant defined its continuity as consisting in this, that between any two points upon it there are points. This is true, but manifestly insufficient, since it holds of the series of rational fractions, the multitude of which is only dinumerable. Indeed, Kant’s definition applies if from such a series any two, together with all that are intermediate, be cut away; although in that case a finite gap is made. I have termed the property of infinite intermediety, or divisibility, the Kanticity of a series. It is one of the defining characters of a continuum. We had better define it in terms of the algebra of relatives. Be it remembered that continuity is not an affair of multiplicity simply (though nothing but an innumerable multitude can be continuous) but is an affair of arrangement also. We are therefore to say not merely that there can be a quantitative relation but that there is such, with reference to which the collection is continuous. Let denote this relation. Then, as quantitative, this has […] these properties:

and

Then the property of Kanticity consists in this:

To complete the definition of a continuum, the a’s, we require the following property. Namely, if there be a class of b’s included among the a’s but all inferior to a certain a, that is, if

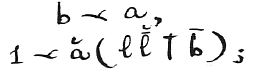
and if further there be for each b another next superior to it; that is,

then there is an a next superior to all the b’s. That is,

I call this the Aristotelicity of the series, because Aristotle seems to have had it obscurely in mind in his definition of a continuum as that whose parts have a common limit.

…a continuum is merely a discontinuous series with additional possibilities.

…time is a continuum. For since the instants, or possible events, are as many as any collection whatever, and there is no maximum collection, it follows that they are more than any collections whatever. They must, therefore, be individually indistinguishable in their very existence – that is, are distinguishable and the parts distinguishable indefinitely, but yet not composed of individuals absolutely self-identical and distinct from one another – that is, they form a continuum. A continuum cannot be disarranged except to an insignificant extent. An instant cannot be removed. You can no more, by any decree, shorten a legal holiday by transferring its last instant to the work-day that follows that feast, than you can take away intensity from light, and keep the intensity on exhibition while the light is thrown into the ash-barrel. A limited line AB may be cut into two, AC and C’B, and its ends joined, C’ to A and C to B. That is to say, all this may be done in the imagination. We have a difficulty in imagining such a thing in regard to time.

…although all my conclusions about abnumerals were brought to ruin, what I now say about continuity would stand firm. Namely, a continuum is a collection of so vast a multitude that in the whole universe of possibility there is not room for them to retain their distinct identities, but they become welded into one another. Thus the continuum is all that is possible, in whatever dimension it be continuous. But the general or universal of ordinary logic also comprises whatever of a certain description is possible. And thus the continuum is that which the Logic of Relatives shows the true universal to be.

A continuum is a system of relations determined by a general rule, which by virtue of its perfect generality does not suppose any ultimate units (indeed such a unit would involve a breach of the continuity, because introducing something not general), but which yet not only permits the distinction of units but provides relations by which any multitude of ultimate units would be perfectly distinguished from one another.

Ah! I had better say a system of connections rather than a system of relations.

Although Kant confuses continuity with infinite divisibility, yet it is noticeable that he always defines a continuum as that of which every part (not every echter Theil) has itself parts. This is a very different thing from infinite divisibility, since it implies that the continuum is not composed of points, as, for example, the system of rational fractions, though infinitely divisible, is composed of the individual fractions. If we define a continuum as that every part of which can be divided into any multitude of parts whatsoever – or if we replace this by an equivalent definition in purely logical terms – we find it lends itself at once to mathematical demonstrations, and enables us to work with ease in topical geometry.

A true continuum is something whose possibilities of determination no multitude of individuals can exhaust. Thus, no collection of points placed upon a truly continuous line can fill the line so as to leave no room for others, although that collection had a point for every value towards which numbers, endlessly continued into the decimal places, could approximate; nor if it contained a point for every possible permutation of all such values.

A collection, or system, is an abstraction or abstract ens; and thus the whole doctrine of number is founded on the operation of abstraction. If we conceive an object to be a collective whole, but to be so in such a way that it has no part which is not itself a collective whole in the same way, then, if the collection is of the nature of a sorite, it is a general, whose parts are distinguished merely as having additional characters; but if the collection is a set, whose members have other relations to one another, it is a continuum.

…I made a new definition, according to which continuity consists in Kanticity and Aristotelicity. The Kanticity is having a point between any two points. The Aristotelicity is having every point that is a limit to an infinite series of points that belong to the system.

I here slightly modify Cantor’s definition of a perfect system. Namely, he defines it as such that it contains every point in the neighborhood of an infinity of points and no other. But the latter is a character of a concatenated system; hence I omit it as a character of a perfect system.

But further study of the subject has proved that this definition is wrong. It involves a misunderstanding of Kant’s definition which he himself likewise fell into. Namely he defines a continuum as that all of whose parts have parts of the same kind. He himself, and I after him, understood that to mean infinite divisibility, which plainly is not what constitutes continuity since the series of rational fractional values is infinitely divisible but is not by anybody regarded as continuous. Kant’s real definition implies that a continuous line contains no points. Now if we are to accept the common sense idea of continuity (after correcting its vagueness and fixing it to mean something) we must either say that a continuous line contains no points or we must say that the principle of excluded middle does not hold of these points. The principle of excluded middle only applies to an individual (for it is not true that “Any man is wise” nor that “Any man is not wise”). But places, being mere possibles without actual existence, are not individuals. Hence a point or indivisible place really does not exist unless there actually be something there to mark it, which, if there is, interrupts the continuity. I, therefore, think that Kant’s definition correctly defines the common sense idea, although there are great difficulties with it. I certainly think that on any line whatever, on the common sense idea, there is room for any multitude of points however great. If so, the analytical continuity of the theory of functions, which implies there is but a single point for each distance from the origin, defined by a quantity expressible to indefinitely close approximation by a decimal carried out to an indefinitely great number of places, is certainly not the continuity of common sense, since the whole multitude of such quantities is only the first abnumeral multitude, and there is an infinite series of higher grades. On the whole, therefore, I think we must say that continuity is the relation of the parts of an unbroken space or time. The precise definition is still in doubt; but Kant’s definition, that a continuum is that of which every part has itself parts of the same kind, seems to be correct. This must not be confounded (as Kant himself confounded it) with infinite divisibility, but implies that a line, for example, contains no points until the continuity is broken by marking the points. In accordance with this it seems necessary to say that a continuum, where it is continuous and unbroken, contains no definite parts; that its parts are created in the act of defining them and the precise definition of them breaks the continuity. In the calculus and theory of functions it is assumed that between any two rational points (or points at distances along the line expressed by rational fractions) there are rational points and that further for every convergent series of such fractions (such as 3.1, 3.14, 3.141, 3.1415, 3.14159, etc.) there is just one limiting point; and such a collection of points is called continuous. But this does not seem to be the common sense idea of continuity. It is only a collection of independent points. Breaking grains of sand more and more will only make the sand more broken. It will not weld the grains into unbroken continuity.

Personally, I agree entirely with James, against Dedekind’s view; and hold that there would be no actually existent points in an existent continuum, and that if a point were placed in a continuum it would constitute a breach of the continuity. Of course, there is a possible, or potential, point-place wherever a point might be placed; but that which only may be is necessarily thereby indefinite, and as such, and in so far, and in those respects, as it is such, it is not subject to the principle of contradiction, just as the negation of a may-be, which is of course a must-be, (I mean that if “S may be P” is untrue, then “S must be non-P” is true), in those respects in which it is such, is not subject to the principle of excluded middle.