Commens

Preliminaries: Alpha, Beta, Gamma

Peirce, possibly the greatest knowledge engineer of the second industrial revolution, developed his magnificent graphical system of diagrammatic logic in three phases. The first part, known as the Alpha part, was inspired, among others, by Alfred B. Kempe’s endeavours during 1870s to improve Euclid’s and John Venn’s graph notation and in trying to prove the four-colour theorem. Its theory is isomorphic to the theory of propositional logic. The second, which came in sequences of two, first as the entitative graphs soon overridden (in 1896) by the dual existential version, is known as the Beta part. Its theory is isomorphic to the theory of predicate logic with quantifiers and identity.¹

As Peirce held anything “extralogical” to be mere shibboleth (2.532, 1893), the third phase, known as the Gamma part, was a cluster of attempts to deal with a variety of notions such as modality, including temporal concepts.² Peirce envisaged several methods to accomplish this, including the classification of predicates that would denote different “potentials” (CP 4.524-526, 1903; MS 508: B.6), and the use dotted closed lines to represent a unary modal operation on graphs in their interior. The Gamma part was also an attempt to reason about graphs themselves as well as to deal with higher-order notions of collections and quantification of properties, such as capturing the precise diagrammatic content of sentences such as “Aristotle has all the virtues of the philosopher”. By doing so, he came to instigate the concept of abstraction, which marked an early anticipation of category theory (McLarty, 1995). Regrettably, he failed to separate these three Gamma compartments from each other (for instance, in defining collections Peirce used the notion of abstraction).

I wish to make two preliminary points concerning these divisions. First, it is not generally known that Peirce projected also a fourth part called Delta, which was by his own words needed “in order to deal with modals” (MS 500: 2-3, 1911). I take this remark to be indicative of the fact that the modal compartment of Gamma was no good in Peirce’s judgement. Whether abstraction or collections fare better has nevertheless not yet been settled by Peirce scholars. Apart from the occasional reference, no further documentation on the planned Delta has survived.

Second, to say that theories of any two systems are isomorphic is a very weak assertion indeed, since it does not imply anything about the iconic aspects of Peirce’s system, which was of central concern for him in devising these graphs in the first place. What iconicity was meant to capture was that the means of representing ought to share the key structural similarities with what it attempts to represent. As the target was to capture a “moving picture of the action of the mind in thought” (MS 298: 1, 1905; Pietarinen, 2003g), he was after similar things as the cognitive scientist using logic in knowledge representation tasks, and the cognitive linguists in regarding meaning as conceptualisation, but a hundred years ahead of them.

Let us review the rudiments of EGs. The fundamental notion in any graph is the Sheet of Assertion (SA) on which graphs are scribed. It provides the universe of discourse, which for EGs is a collection of individuals. A blank SA on which nothing is drawn represents a zero-place constant of the truth. The earlier entitative graphs were duals to this and so a blank SA represented falsity.

The basic operation in both the Alpha and the Beta is composition (or juxtaposition) of graphs and atomic nodes termed spots. Peirce took composition to be analogous to Boolean conjunction. The spots, together with their hooks in the Beta case, are uninterpreted (“unanalysed”, CP 4.441) atomic propositions, typically linguistic expressions or rhemas that have blank lines of expression (MS 491: 3-4, c.1903). Taking juxtaposition to define isotopy-equivalence classes, it is clear that the orientation of juxtaposed graphs on an SA does not matter for truth or falsity and conjunction is commutative and associative.

The other basic operation is the cut, which is a closed simple curve around a graph, including atomic spots. Peirce took this operation to be analogous to Boolean negation. The operation is iconic in the sense that it severs its interior area from the SA and thus asserts the denial or a mirror image of what the area contains. What remains on the sheet is the place of the area of the cut (MS 514: 8). Thus, a cut drawn on a blank SA represents a zero-place constant of falsity.

By way of a simple example, (1) is an example of an Alpha graph that represents the proposition (2):

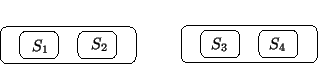
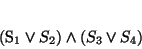
Moving on to Beta graphs, the third key iconic sign that Peirce introduced was the Line of Identity (LI). It connects spots such that any spot is understood to have a periphery, upon which a finite number of imaginary hooks are pictured, and to which an LI may connect. If an LI does not connect to a hook, its unconnected extremity is a loose end. An LI that connects to only one hook and does not have a loose end reduces to a zero-dimensional dot. He took it to be analogous to existential quantification. Iconically speaking, a dot on an SA singles out an individual subsisting in the universe of discourse. At most one LI or a dot may occupy a hook – hence the irreducibility of triadic relations. Counting the number of connections at the periphery of a spot corresponds to the number of arguments of a predicate. LIs may be connected to each other, and the totality of connected LIs gives rise to a ligature. Any line that crosses a cut is a ligature composed of two lines. Like subgraphs, LIs in ligatures are compositions read as conjunctions (e.g., “there exists b and this b is not S”). Connected to a predicate, lines of the same length and with a loose end give rise to an isotopy-equivalence class, and thus their order is irrelevant. This is in accordance with Peirce’s remark that, “If either proponent or opponent has, at any stage, several individuals to select successively, it is obvious that the order in which he names them will be indifferent, since he will decide upon them in his own mind simultaneously” (MS 430: 62, 1902).

According to Peirce, the interpretation of existential graphs is endoporeutic, in other words the flow of information is from the outside in: the outermost occurrence of a graph is examined first and the examination proceeds stepwise towards terminal graphs, which are either rhemas (predicate terms), a verum, (i.e. an empty sheet), or a falsum (i.e. a cut around an empty sheet). The outermost existential quantifier in a predicate logic formula would be denoted by a line of identity in the outermost zone of the graph. The implication is symbolised by two nested circles (termed by Peirce the scroll), the outer one denoting the antecedent and the inner one denoting the consequent. For instance, the following beta graph

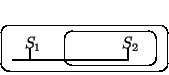
with two cuts, two rhemas (predicates) S₁ and S₂, and one line of identity abutting a cut, asserts that, given any individual object of the universe of discourse of which S₁ is true, S₂ is true. The two nested cuts denote implication, and the heavy line of identity asserts at its outermost extremity that there is an individual that we are speaking of in the universe of discourse. Its continuation all the way to the inner extremity, abutting the inner cut and ending at S₂ , asserts that this individual is identical (“numerically identical”, MS 513: 54, n.p., n.d., untitled) to the one of which S₂ is true. The something at one end of the line is “the very same individual” (MS 514: 50) as the something at the other end. The gamma part lies outside the scope of this article (Roberts, 1973).

Model theory

It has not been widely recognised that in his EGs, Peirce came up with a version of what has subsequently developed under the auspices of model theory. The invention of model theory is habitually credited to people such as Alfred Tarski, Anatolii Mal’tsev and Abraham Robinson, who, in the 1950s, proposed the term for the mathematical discipline that had emerged sometime earlier, most notably during the phases of discoveries in mathematical logic at the beginning of 1930s.

Tarski’s purpose was to develop a formal language such that any of its expressions having the same meaning can always be replaced for each other. (Peirce would have spoken of signification instead of meaning.) There were a number of other requirements, too, which I will not discuss here. In model theory, the interpretation A of a sentence S of a language L, by a mapping of non-logical and logical symbols of S to a domain of a structure, is called a model of S, if it makes S true in A. The inverse of this mapping provides an assignment function. Thus the basic predicates, constant symbols and function and relation symbols (if there are any) will acquire an interpretation. Predicate and relation symbols with a fixed arity are interpreted on the product of the relations of the domain, and the constant symbols are interpreted by assigning them an element of that domain of discourse. Furthermore, assignments so defined need to be extended to valuations assigning values also to the variables of the non-logical alphabet.

Peirce’s dialogical interpretation

Peirce’s dialogical interpretation enters the picture here. In EGs, the work of assignments is done by the players who choose objects from the universe of discourse so that they fit the intended statement. As the interpretation A that delineates a specific class of objects is a structure, and as in Peirce’s existential graphs a sentence S is scribed in diagrammatic form as an existential graph G, the structure that interprets G is another graph G’ onto which G is homomorphically mapped. It is from the universe of G’ that the players choose objects to which the expressions in G refer, and which fit the statements intended by them.

The function of the unextended assignment was understood by Peirce to be all that which is mutually agreed to exist and known to be mutually agreed by the Graphist and the Grapheus (or by the utterer and the interpreter if we step outside the iconic contexts of the diagrams into his overall semeiotics). However, before values (proper names, indefinite names, selectives) may be chosen and attached to the dots or identity lines hooked to the predicates, the domain will have to come with a (non-exhaustive) supply of names for the individuals, and the players would need to have a basic understanding of what the rhemas with blank forms of expression are intended to mean, in order to work as expressions that possess `semantic attributes’, and thus constituting parts of propositions with definite truth-values.

As it happens, the sheet of assertion is such a mutually understood universe. It is not just a domain of individuals, but also an interpreted structure on which complex assertions can be scribed and their status determined according to the truth and falsity. In modern terms, it is the τ -structure of the domain, where τ (the set of basic symbols of constants, predicates and relations), onto which the scribed graph is mapped by the inverses of the actions taken by the Graphist and authorised by the Grapheus.

How the non-logical constants will receive their interpretations was not for Peirce, unlike for later model theorists, the result of any process of fixing a model. It is part of the ‘natural history’ of logic. Only via such history interpretations may be determined, through conditions attached to sound thought. That constitutes the starting point of logical inquiry, the point where all study lies open before us. Peirce explains thus:

The reason that unextended assignments are no matter of trivial definitions is due to Peirce’s emphasis on pragmatics, namely on logical propositions as assertions put forward in communicative situations. This emphasis on assertoric content and the responsibility of the utterers and the interpreters of their own assertions gets stronger the closer we come to his last writings. In about 1910 he wrote, in shaky hand,

Further details of Peirce’s dialogic and communicative approach to interpretation are found in Bergman (2000); Johansen (1993); Pietarinen (2003a,b).

The endoporeutic method

The dialogic interpretation is, in brief, is Peirce’s model theory, also known as the endoporeutic method in the context of existential graphs.³ The term “endoporeutic” (adj., cf. “semantic”) appears in few places, however.⁴ In MS 650: 18, 19 [24 July 1910], Peirce speaks about “endoporeusis” (“inward-going”) and the system of graphs expressing the truth “endoporeutically”, and in MS L 477 [1913], he uses the adverb “endogenously” as a substitute. Following the morphology of ‘semantics’, let us coin the noun ‘endoporeutics’.

Related to these remarks is CP 4.408 [1903], where Peirce notes that, in general, the interpretation should proceed from the outermost occurrences of selectives towards the insides of the cuts. All this means one and the same thing: the interpretation of existential graphs proceeds in an outside-in fashion, starting with the outermost graph replica or outermost extreme of a ligature and proceeding towards the innermost replicas. Each step, performed either by the utterer or the interpreter of the graph, peels off one instance, until the atomic instance is left. If there is a cut, the choice of an object from the universe of discourse is transferred to the opponent of the current player.

Statements explicating endoporeutics are nevertheless conspicuously rare. This is a gap in Peirce’s writings, and some crucial definitions and passages have been lost. For instance, among the dozens of technical terms in his index to Prolegomena (MS 292: subjacent to page 53), he included “Endoporeutic Interpretation”, which was to be found in “531, 23-28” (Peirce’s own numbering and pagination).

The term appeared for the first time around 1905, the same year he spoke about “working models” (MS 298: 5), the conception created by the mind’s relation to graphs. However, he had already noted in 1903 (MS 491; CP 4.408) that there was a rule for existential graphs according to which what is scribed outside an enclosure in a graph is always mentioned before what is inside of it. The sentences in 514: 16 [1909] read:

The reference to shaded and unshaded areas was his alternative notion for negation, which he later changed from a simple closed line to the shading of the area on the sheet of assertion that denotes the graph replica that is negated.

The principle of endoporeutics was not only semantics – to abuse the more current signification of that term - but it also entitles the proof-theoretic rules of iteration and de-iteration:

The “nest” is a technical term meaning the sequence of cuts from those that have the largest number of enclosures to those that have the fewest. It corresponds to the total history (complete path from the root to the terminal history) in the extensive-form representation of existential graphs (see below). As the rules of iteration and deiteration are what we nowadays perceive to be proof-theoretic, it is interesting to note how Peirce thought them to be parasitic on semantic (model-theoretic) considerations.⁵ Admittedly, he spoke of diagrammatic “Syntax” being “endoporeutic” (MS 669: 4), but this was façon de parler, as by that he meant that lines of identities are understood so that they are interpreted in the outside-in order.

The remark Peirce makes about the “endogenous” interpretation of existential graphs is interesting because there he considers the opposite possibility, that of an “exogenous” interpretation as well.⁶ Nevertheless, in his judgement an exogenous interpretation that begins in the inside and proceeds outwards is not to be preferred, because the nested system of cuts (here as in the other examples of shaded graphs) that are read as implications – as in the case when there are two nested cuts, A lying on the shaded area and B in the non-shaded area inside the shaded one, read as ‘If A is true so is B’ (or equivalently, ‘It is false that A is false while B is true’) – would not assign a proper meaning to implications when read inside out, which in the case of this example amounts to ‘B is true and A is false’, contradicting the example. Further textual instances are found among the assorted pages of MS 295. Peirce writes on page 83:

And on the assorted page 87 that

This latter statement particularly significant, because it asserts that the order of interpretation also concerns the areas of the cuts and the places upon which they are asserted but severed from. It is via this ordering that the context-dependency of all that is scribed on the areas of cuts is secured. The latter quotation is embellished in MS 300: 48 as follows:

Again, Peirce is absolutely clear about the requirement that whatever lies in the context must not be lost in the interpretation.

According to Peirce, “Endoporeusis, or inward-going” (MS 650: 18), is like a global clock that synchronises interpretation and arranges it in a definite inside-out order. It is like

Further facets of endoporeutics

That truth-conditions established by the endoporeutic method were one of Peirce’s central concerns in his logic is shown, for one thing, in the slightly earlier remark, “Logic proper is the formal science of the conditions of the truth of representations” (CP 2.229, 1897). He expressed this in MS 593 [n.p., 1893] by elaborating on what the conditional proposition ‘if A is true, B is true’ means:

He refers to the notion of the possible state of things as a universe that consists of a range of possibility. The invoked labyrinth of modalities was to haunt his logical investigations for the better part of his days (Pietarinen, 2003h). Besides thus vindicating his model-theoretic and dialogic attitude to existential graphs in terms of endoporetutics, he also defined logical equivalence in model-theoretical terms by noting the following.

This is a remarkable statement, especially in light of the fact that conceivable cases are what are nowadays perhaps best viewed as classes of models. What Peirce is vaguely anticipating is categoricity (descriptive completeness) of a logic, in other words the uniqueness of models up to isomorphism.

From this definition we also see what Peirce intended logical consequence to be. It is a relation between an antecedent formula and a consequent in which there are no conceivable cases (models) in which the former is true and the latter is false.

Furthermore, in NEM 2:517, Peirce remarks, “In order to demonstrate that any collection A, is greater that any collection B,it is useful to think of the relations τ that these collections bear to each other as producing a “character”“, which in turn gives rise to a situation which can be thought of as “a sort of diagram, or model, in which we think of the Bs as so may boxes, the As as so many bullets, and the relation τ as that of containing”. Here Peirce even uses the term ‘model’ in relation to some conceivable iconic situations, albeit in the context of measuring the multitudes of collections.

Peirce’s overall approach to iconicity in existential graphs may be seen as the proper use of signs as their own models. This is not only an instance of hypostatic abstraction, but also resembles the semantic techniques that use maximally consistent sets in proving completeness results for given calculi; techniques developed much later by Leon Henkin and many other logicians, essentially using sets of sentences as the models of sentences.

During the last months of his life, Peirce amended the analytic use of diagrammatic methods by noting that every logical term has to be linked or bound to “one real universe” (MS L 477: 11r, 14 Oct 1913). This is represented in graphs by scribing terms on the sheet describing the universe. The idea of “being bound to the real universe” comes very close to the model-theoretic idea of being able to speak about interpreted statements by mapping the terms of one’s language to the domain of the structure. Peirce claimed to have been struck by this idea in a rejected paper written in January 1897 for The Monist, which is indeed the manuscript in which the theory of existential graphs was inaugurated.

However, the structures that he had in mind were not set-theoretic, but were applied to any of the more general diagrammatisations intended to capture iconically any thought that the mind produces. In actual cases, these signs are mainly assertions, but also non-declarative moods of commands, questions (in interrogative inquiry), music, imaginations and absurdities were contemplated. Virtually anything that is linked to the mind or the quasi-mind ought to be subsumed to similar iconic and model-theoretic scrutiny.

Thus Peirce not only came to provide an early version of model theory and a fresh incentive for its later advancement, he also recognised the importance of the iconic character of linking scriptures to structures in logical graphs. The importance of the iconic view of logic is well beyond the mere symbolic and even the received model-theoretic conceptions.

This hints at the idea of ‘mental models’, familiar from cognitive science (Johnson-Laird, 1983). According to this theory, the mind constructs a range of scenarios, models or pictures to accomplish reasoning and in making decisions. Hodges (1993) has criticised the theory of mental models on the grounds that it has nothing to do with the kind of model-theoretic reasoning and argumentation that mathematical model theory provides. Both accounts are misguided. Peirce was using a model theory for his theory of existential graphs roughly fifty years before Tarski suggested the name for what was regarded at that time a relatively recent mathematical discipline, and roughly thirty years before model-theoretical methods infiltrated mathematical and symbolic areas of logic. But such a model theory is bound to remain deficient if it does not approve the creative links with various diagrammatic and iconic systems of representation there are in thought and cognition. The reason is the almost total expurgation from recent logical theories of what Peirce would have considered the most important part of logical reasoning, the category of secondness, and the ensuing triadic relation of logical signs to the minds of their interpreters.⁷

The diagrammatic and graphical method of drawing these links has turned out to be effectual, not only because it allows one to intersect cuts (negations) by ligatures composed of a continuous collection of lines of identities, but also because one can symbolise any η-ary relations by them. According to so-called Peirce’s reduction thesis, all relations with an arity of four or more are reducible to triadic relations, called teridentities. Furthermore, the diagrammatic notation literally forces the interpretation of graphs to be an onion-like process that proceeds from the outermost occurrences towards inner, contextually constrained occurrences. (He argued that diagrammatisation implied “Endoporeutic Principle”, MS 293: 53, c.1906.) The ligatures are not graphs because they may involve some discontinuous, non-compositional parts, not definable by inductive construction. That these lines depict the existence of individuals is merely a by-product of the way in which they cope with the other, more primary topological and continuous notions such as interaction with predicates (predication). One consequence is that continuity in diagrams unifies the different senses of ‘being’ and puts them under equal logical and diagrammatic scrutiny.

Model-theoretic seeds are also discernible in Peirce’s more general writings, such as his late Reflexions upon Reasoning (MS 686, n.d.). In that and in much of his work from the last years of his life he tried to tackle the nature of reasoning from several synthesising points of view, making use of the prevailing notions of modalities, assertions, as well as the distinction between logica utens and logica docens (see the entry ‘logica utens’; Pietarinen 2003i). He wanted to connect reasoning with the notion of “the state of things”. The state of things is a mental concept which, by being conceivable itself, gives rise to further possible and conceivable states of things, again which realise further states, and so on. Thus it is not an objective construct required of models in the mathematical sense. By a state of things Peirce nonetheless meant “anything the reality of which might constitute the truth of an assertion” (MS 686: 1). Truths of asserted propositions thus have to be contemplated in some given or produced state of things at the time, not in the whole being. Reality itself is not the totality of all there is. By it “is to be understood that part or ingredient of the being of anything which does not depend upon that thing’s actually being represented” (MS 686: 1). In this case, states of things have their real or objective counterparts.

While this account of the truth of an assertion in a state of things may resort to notions of modality and possibility, it is actualised as soon as the principles of contradiction and the excluded middle are applied. For Peirce, the outcome of having such states was a guarantee that logical reasoning is necessary and certain, not open to doubt. In order for reasoning to be reliable, the assertion must hold not in a single state of things, but in all states of things, in something of which we have “a trustworthy knowledge of what would always be true” (MS 686: 6).

Graphs, contexts and compositionality

The upshot is that endoporeutics instruct us to refer to contexts rather than to scopes in EGs. This term has indeed been adopted in research on conceptual graphs in AI and computer science (Sowa, 2002,1984), and for reasons brought out by the pragmatic aspects of graphs as representations of assertions, is increasingly being used in computational tasks related to speech recognition in dialogue systems.

This emphasis on the contextual viewpoint was well recognised by Peirce. Unfortunately, the context dependence has not been invariably applauded. Customarily, it has been downplayed because it hampers what many regard as the essential ingredient of not only any feasible logical system, but also of the ‘guilty secret’ logicians and linguists may have concerning natural language (Sandu & Hintikka, 2001), namely compositionality. If proper subgraphs or subformulas are context-dependent, they do not necessarily have a self-supporting meaning, contradicting the programme that Tarski had in mind. For this reason, they are not proper constituents of any larger unit, typically a formula or a sentence, whose meaning ought to be morphically imaged on those constituents, the advocates of the compositional approach will profess.

According to Shin (2002), Peirce’s obsession with endoporeutic interpretation in fact has foiled a comprehensive understanding of his system and its setting in a wider perspective. Is this a plea for compositionality? Shin does not use such a term, but says that no challenge has been made to the endoporeutic method of reading graphs. It does not “reflect visually clear facts in the system”, and in fact “forces us to read a graph in only one way” (Shin, 2002, p. 63).

What are these visually clear facts? Shin refers to the impossibility of reading graphs so as to determine which are oddly enclosed and which are evenly enclosed by cuts. While this endoporeutic reading may give correct truth conditions for graphs, nested cuts are often needlessly forced to be substituted by corresponding implications. There is no mention in such a reading of a disjunction, namely the juxtapositions of encircled subgraphs within an even number of cuts. Likewise, no vocal difference obtains between existential and universal quantification in the endoporeutic outside-in reading of graphs.

These remarks made by Shin in fact reflect wider and more far-reaching issues. She terms the preferred reading a “direct reading” or a “multiple reading”, while the endoporeutic reading is “indirect”. Similar terminology was employed by Keith Stenning in his discussion on the iconic nature of diagrammatic methods (Stenning, 2000). There is no mention of the dialogical, communicational interpretation of graphs in these works. I strongly doubt that a comprehensive overview of existential graphs can be obtained without such an interpretation. For instance, the difference between existential and universal quantification is precisely that which determines which one of the parties, the Graphist or the Grapheus is to choose an instance from the universe of discourse as intended by the proposition depicted by the graph. The switching between them is then facilitated by the system of cuts. Likewise, the distinction between reading the graphs as representing conjunctions and reading them as representing disjunctions amounts to this role-playing view of dialogical or game-theoretic interpretation.

The absence of two interlocutors is a symptom of a more general presupposition concerning logic and language, compositionality. This assumption that has preoccupied a number of logicians and logically minded linguists in their search for suitable expressive representations. The communicative and dialogical interpretation of existential graphs shows what is ill conceived in such preoccupations. Given a full endoporeutic interpretation of graphs, there is nothing missing in the way these graphs are read, as the distinction between different quantifiers and different logical connectives is exposed by the system of choices performed by the utterers and the interpreters associated with the graph, the meaning of which is to be disclosed.

Another way of putting a closely similar point across is to note the equivocation in Shin’s use of the term endoporeutics and Peirce’s use of it. Shin speaks about the “endoporeutic reading” of the graphs, while for Peirce, the endoporeutic principle was not a matter of reading the graphs, but a necessary follow-on from the diagrammatisation that dictates how to interpret them. This principle provides with a method for expressing the truth of the graphs, and consequently a method for reading them. A full understanding involves the usage of the two interlocutors, who choose and assign semantic values to each component in a certain order that respects the passage from the outer instances to the inner, contextually constrained instances. This order can be unambiguously spelled out in the game-theoretic interpretation (see below), and it is implicit in Peirce’s notion of “nests” of graphs (CP 4.472, c.1903; CP 4.494, c.1903; CP 4.617, 1908).

Peirce nevertheless thought the meaning of EGs to be compositional in the sense of being determined by its component graph-instances. This is evidenced in MS 280: 35, in which he wrote, “The meaning of any graph-instance is the meaning of the composite of all the propositions which that graph-instance would under all circumstances empower the interpreter to scribe”.⁸ The reasons for holding this assumption are less clear, however, given the fact that the system of graphs is entirely contextual in the sense that any cut that is scribed on the sheet will create a context for the diagrammatic subexpressions occurring within its enclosure. There are no partial overlaps, and any graph can thus be represented in a tree format. If there is such a heavy iconic reliance on nested systems of contexts, however, it is but a small step to extensions that assume the possibility of transforming a graph into a partially ordered set rather than a tree structure. These extensions are no longer compositional, but as the graphs in question are all finite, there is always a possibility of devising an interpretation that is compositional, provided that one carries all the requisite contextual information within the subgraphs that are to be interpreted prior to the larger graphs within which they are embedded.

There is a dazzling juncture at which Peirce comes close to the possibility of non-compositional graphs, however. In MS 490 [1906] he discovered a graph that crosses a cut. In one of his multiple attempts to capture modalities by gamma apparatus, he found that comparisons between actual and possible individuals could not be avoided. There is a need for representing assertions concerning identification (or non-identification) between existent things scribed on the blank sheet and possible things scribed on the shaded enclosure of a cut (corresponding to the enclosure of a broken cut in the alternative notation), that is, on a graph that refers to the universe of possibility. In that case, a line of identity and not a ligature exists that signifies such an identity. Thus, a graph that crosses a cut exists.

This, briefly, is the explanation of what Peirce means in CP 5.583 (a fragment of MS 490) in his assertion that there are concepts that are not propositional. As he noted in 5.583, non-propositional signs can only exist as constituents of propositions, while it is not true that a proposition can be built up of non-propositional signs. A non-propositional sign is one that is not being assigned a semantic attribute, or a meaning, by either of the interlocutors. In this sense, it violates compositionality, because one version of this principle asserts that the meaning of the proposition has to come from the meaning of its constituents and their proper combinations. According to Peirce, no proposition can be properly assembled from non-propositional signs alone.⁹

The question for Peirce was not how to read off what the graphs are intended to convey. There may be more than one way of doing that. The question was how to express truth “endoporeutically” (MS 650: 19). He predicted that “if anybody were to find fault with the system … I should be disposed to admit that it is a poetical fault” (MS 650: 19). In pure aesthetic terms, there may be alternatives, but such alternatives ought to accomplish at least as simple a set of rules as endoporeusis does, and in addition predict the same merits of its essential features.

However, suggested alternatives to the endoporeutic method of interpretation have not fulfilled these predictions. Shin’s proposal to reduce alpha graphs to the negation normal form involves a recursive definition starting from atomic graphs outwards. Replacing Peirce’s five conventions of erasure, insertion, iteration, deiteration and double cut, Shin’s reformulated inference rules come in seven parts, four of which are partial decompositions of the rules of iteration and deiteration into the rules that have been in use in natural deduction systems.¹⁰ Albeit much more complex in the case of beta graphs, there are still the five conventions for their transformation, which Shin reformulates into nine rules divided into twenty-five subcases.

Since Peirce garnered the processual component of dialogical interpretation from the extended notion of an assignment, he would not have run into similar difficulties as one does in cases where the single assignments no longer work as adequate interpretations for subexpressions. This happens precisely in cases where the underlying language is not compositional. To interpret formulas of such a language compositionally, one needs to extend the assignment for each subformula or a component into a set of assignments in order to cope with the “would-be” interpretations that such non-compositional ectoporeutically or endogeneously interpreted subexpressions need to assume. One drawback is that such an interpretation increases immensely the complexity of the semantics, making it for that reason unnatural.

In general, then, compositional methods of interpretation are far more complex in that they are liable to have a considerably larger number of transformation rules than Peirce had. Furthermore, new extensions are bound to increase the complexity of any compositional alternative.

Graphs as games

Endoporeutics is closely related to game-theoretic semantics (GTS) of Pietarinen (2003c); Hintikka & Sandu (1997); Hintikka (1973). This connection was observed in Hilpinen (1982). A mapping of alpha part to GTS proposed in Burch (1994). Generally speaking, to get semantic games from Peirce’s dialogical interpretation of existential graphs, the Grapheus and the Graphist are mapped on their roles of NATURE and MYSELF, respectively. The mapping is total, that is, at each non-terminal history of the game a player has one of these roles and the adversary has the other.

As in endoporeutics, players start from an out-most cut or a graph outside a cut, and proceed towards an atomic or a blank graph. At each point at which a decision is to be made, an erasure is performed, that is, a cut is removed or a player throws away the graphs that were not designated. When the cut is encountered, the roles of the players will change, and the winning conditions will also change throughout the examination. Since the graph is finite, an atomic graph is eventually reached. The winning conditions are such that when an atomic graph is reached, the player playing the verifying role (i.e. MYSELF) wins if that graph is true or is a blank one, and the player playing the falsifying role (NATURE) wins if that graph is false or a blank one encircled by a cut.

The molecular graph itself is true precisely in the case when the player who made the first move as MYSELF is able to win no matter how her adversary moves. Symmetrically, the graph is false precisely in the case when the player who made the first move as NATURE is able to win no matter how his adversary moves. In the terminology of semantic games, we say that, in these cases, there exists a winning strategy for a player.

In the case of the beta part of the theory of existential graphs (not covered in Burch 1994), there are, in addition, lines of identities. Among other things, these correspond to existentially quantified variables, identities between the variables, and the relation of coreference. Accordingly, their interpretation is such that suitable individuals have to be picked from a domain of discourse by MYSELF and assigned to the corresponding lines. To do this, we need to assume that there is a domain of individuals and they have been arranged so as to form an interpreted structure. An interpretation consists of a structure with a non-logical alphabet attached to the domain and definite valuation given to the terms and predicates.

Similar winning conditions and truth definitions apply to beta graphs as to alpha graphs, with the addition that the atomic graphs are also interpreted by the Grapheus in terms of checking whether the sequence of individuals chosen during the endoporeutic interpretation are to be included in the extensions of the atomic predicates that have been reached at the terminating atomic spots. If so, the current player who is MYSELF will win. If not, the player who is NATURE will win.

Since Peirce did not have the concept of a winning strategy at his disposal, he was content with using descriptions such as the following:

Here strategic reasoning permeates logical tasks. In other words, attainment of the notion of the finality of interpretants furnishes the maximalisation of the utilities that are the outcomes of actions suggested by the minds of the communities of self-controlled agents. The result of self-control that amounts to the development and evolution of behaviour, and ultimately to the increase in the summum bonum of inquirers, is a habit change, here realised in the guise of “definite general tendencies of a tolerable stable nature”.

In order to arrive at extensive games, these conventions are further applied so that we take the root of the tree to be labelled with the entire maximal composite graph scribed on the sheet of assertion, and each choice prompted by the above conventions then extends this root history in an obvious manner (see Pietarinen 2003c for more detail). A terminal history is then one that cannot be extended. Each terminal history is mapped to its payoff, which gets its value from the set {-1, 1}, determined by the Grapheus. These values show which of the plays are wins and which are losses. Any strategy that invariably leads the falsifying (resp. the verifying) player to the terminal history with the payoff -1 (resp. 1) will be a winning strategy for the player of that role. The set of such strategies shows whether the entire graph is true or false according to the principle of endoporeutic interpretation.

The requirement ‘according to the principle of endoporeutic interpretation’ is actually vital, because it almost translates into ‘being true or being false in a model’. The closest Peirce ever gets to this term is his “working model” idea of cognition (MS 298: 5). He intended existential graphs to be true models of moving images of thought. Behind this idea, the intention to interpret graphs ‘in a model’ is nonetheless unmistakable. Just as an interpretation of a sign can be another sign, the role of the model in question is played by another existential graph (i.e. an interpreted structure), which is the homomorphic image of the object graph. The choices made by the players from the universe of discourse of this model graph are converses of the assignments of the values to the components of the object graph.

In contrast to models of model theory that extend to an infinite depth, those conforming to the endoporeutic interpretation are finite in nature. However, there is no principled mathematical reason why they could not be held extendible to approximate standard, infinite, non-extendible models.

The joys of endoporeutics

Unlike the received ectoporeutic (Tarski-type) interpretation, its older brother provides a versatile context-dependent system. Furthermore, it can be adjoined to background knowledge by known AI and computational knowledge-representation techniques such as scripts and frames, default reasoning, and many others. Such information may be encoded into the strategy functions of the game. From this perspective, the contextual meaning remains semantic in its basic nature. The reciprocal nature of “common familiar knowledge” (MS 611-614, 1909) was one of Peirce’s main concerns in bringing out the congeniality of ‘semantic’ and ‘pragmatic’ sides of logic (Pietarinen, 2003e).

What also makes the endoporeutic method, or a semantic game, appealing is that it provides concrete systems in the sense of being potentially playable by real persons or real players. This does not mean that these games are necessarily played by humans, analogously to the socially tedious senses of `the games people play’, although the possibility of applying actual human players is not ruled out. This means that there are several crucial aspects that should be taken into account in the design of systems of diagrammatic logic, which would enable these games to be played by any non-omniscient theoretical entity or agent with limited or bounded resources. These aspects include the following:

• That the graphs are finite, which indeed is the case as the propositions themselves are finite in length. Thus the interaction will come to an end in a finite number of steps, and thus also the plays of the game are all finite.
• That the domains may be infinite, which makes the breadth, not the length, of the game tree infinite.
• That the players are not totally acquainted with the domain on which they pick elements, and are allowed to name the objects when the need arises, i.e. if their identities are not known. In other words, the universes are not total systems sealed off at the outset.

All these requirements may be readily found in Peirce’s logical system of graphs, and in his dialogical interpretation. For instance, with regard to the first item, let us single out the following remark:

It needs to be kept in mind that this finiteness is restricted to the dialogues within the diagrammatic logic, and not, for example, to principles of semiosis or scientific investigation, which Peirce observed to constitute never-ending processes.

Secondly, the universes of discourse may be infinite. It is only the length of the histories associated with the systems of nests that are finitely long. He did not suffer from a bad conscience like other up-and-coming mathematicians such as L. E. J. Brouwer in using infinitary constructions in mathematics. This is shown by Peirce’s concept of existence, which virtually springs from active processes in thought and thinking. Hence a constructive outlook on logic and mathematics was practically forced on him. Logic and mathematics operate with entities that are dependent on the contents of the mind. The contents may be rendered visible by the distinctness of topological diagrams and the character of the working models in which they are evaluated. Such diagrams are best interpreted endoporeutically, and hence Peirce came up with the semantic and model-theoretic method akin to the game-theoretic one.

As regards to the third item, since the Grapheus is “the creator of the universe” (MS 491: 3, c.1903, Logical Tracts. No. 1. On Existential Graphs), he may change characters of the domain of discourse at will. However, the Graphist and the Grapheus are in a communicative relation with each other.

Peirce continues this: “An authorization once given is irrevocable: this constitutes the universe to be perfectly definite”. Being perfectly definite and perfectly determinate are not the same thing, for: “Should the graphist risk an assertion without authorization, he must hope to receive and authorization later; for what never will be authorized is forbidden: this constitutes the universe to be perfectly determinate” (MS 492: 17 a.p.). If it happens that a modification needs to be made to the asserted graph, it has to be made according to sound rules of transformation.

The usefulness of endoporeutics is beyond dispute in numerous applications such as in interpreting anaphoric expressions (not only nominal ones but also those involving temporal coreferences). For how otherwise can the values of anaphoric pronouns be brought into being in discourse than by looking up what has happened in previous rounds of interpretation, interspersed with contextual and environmental matters that the Phemic Sheet, all that is well understood between the utterer and the interpreter, is presupposed to provide?

Similar remarks on contextuality apply to Peirce’s theory of proper names.

Conclusions

Dialogues, habits of evaluation, and the method of endoporeutics alike may be seen as instances of the category of thirdness in logic. Because of the thoroughly iconic nature of diagrams and the strategic, dialogic process taking place between the Grapheus and the Graphist is not in tension with the category of thirdness and the irreducibility of triadic relations.

In the light of post-Peircean developments in logic, an oversight just as unfortunate as underrating the general impact of communicative and dialogical aspects on his logic, has been the unwise exclusion of thirdness from the provinces of 20th-century semantic and model-theoretic approaches to logic. This was a tendency in the writings of his contemporaries, most notably those that he considered to be allotted the epithets of ‘symbolic’ or ‘formal’, that worried him. Here, of course, formal refers not so much to the mathematical component of logic than to the tendency of manipulating formulas by rules of inference that disregard the interpretation of their non-logical constants. The fact that diagrammatic logical graphs and dialogical thinking reveal fundamentally the same phenomena is expressed by Peirce as a requisite in order for the reader to

Peirce’s motivation for such an allegory was his view of thought as presenting moving images of actions of the mind. He elucidates this in his MS 298 immediately preceding the previous extract by offering a twofold approach to the structure and working of thought, namely one endowed with the distinctness of geometrical diagrams plus the convincingness of “working models”. The editors of the Collected Papers (vol. 4) regrettably omitted this important qualification to the distinctness of geometrical diagrams from the publication of the relevant paragraphs of The Simplest Mathematics. This is unfortunate, not least because it is related to the idea of diagrammatic logic as ‘moving pictures of thought’ but because the concept of working models turned out to be the culmination point in the run-up to one of his most spectacular discoveries in logic, his endoporeutic method.

References

Endnotes