Let us now consider what is meant by saying that a line, for example, is continuous. The multitude of points, or limiting values of approximations upon it, is of course innumerable. But that does not make it continuous. Kant defined its continuity as consisting in this, that between any two points upon it there are points. This is true, but manifestly insufficient, since it holds of the series of rational fractions, the multitude of which is only dinumerable. Indeed, Kant’s definition applies if from such a series any two, together with all that are intermediate, be cut away; although in that case a finite gap is made. I have termed the property of infinite intermediety, or divisibility, the Kanticity of a series. It is one of the defining characters of a continuum. We had better define it in terms of the algebra of relatives. Be it remembered that continuity is not an affair of multiplicity simply (though nothing but an innumerable multitude can be continuous) but is an affair of arrangement also. We are therefore to say not merely that there can be a quantitative relation but that there is such, with reference to which the collection is continuous. Let 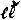 denote this relation. Then, as quantitative, this has […] these properties:
denote this relation. Then, as quantitative, this has […] these properties:
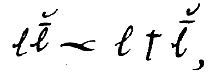
and
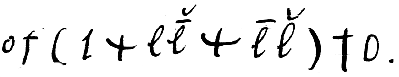
Then the property of Kanticity consists in this:
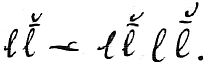
To complete the definition of a continuum, the a’s, we require the following property. Namely, if there be a class of b’s included among the a’s but all inferior to a certain a, that is, if
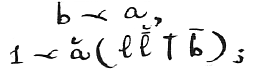
and if further there be for each b another next superior to it; that is,
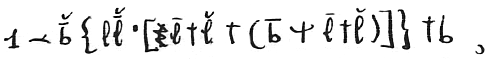
then there is an a next superior to all the b’s. That is,

I call this the Aristotelicity of the series, because Aristotle seems to have had it obscurely in mind in his definition of a continuum as that whose parts have a common limit.